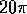 Hz
Hz
1. A wave is described by y(x,t) = 0.1 sin(3x - 10t), where x is in meters, y is in centimeters and t is in seconds. The frequency is:
A) 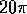 Hz
Hz
B) 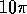 Hz
Hz
C) 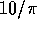 Hz
Hz
D) 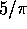 Hz
Hz
E) 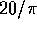 Hz
Hz
In this problem, 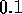 is the amplitude, k=3\
(the angular wave number) and
is the amplitude, k=3\
(the angular wave number) and 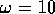 rad/s (the angular
frequency). Then
rad/s (the angular
frequency). Then

The correct answer is D
2. Below are sets of values for the spring constant, damping constant, and mass for a particle in damped harmonic motion. Which of the sets takes the longest time for its mechanical energy to decrease to one-fourth of its initial value?
A) 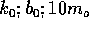
B) 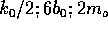
C) 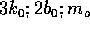
D) 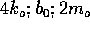
E) 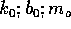
The damping time is set by 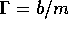 and, as shown in
the formula page, by
and, as shown in
the formula page, by 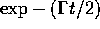 .Large values of
.Large values of
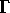 mean rapid damping. Therefore, we are
looking for the SMALLEST value of
mean rapid damping. Therefore, we are
looking for the SMALLEST value of 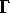 among the various
choices. In A),
among the various
choices. In A), 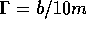 , in B)
, in B) 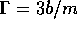 , in
C)
, in
C) 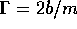 , in D)
, in D) 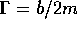 , and in E)
, and in E) 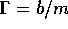 . Clearly in case B)
. Clearly in case B) 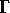 has the largest
value and in case A)
has the largest
value and in case A) 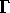 has the smallest value! The larger
the value of
has the smallest value! The larger
the value of 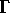 , the more rapidly the energy dissipates.
Conversely, the smaller the value of
, the more rapidly the energy dissipates.
Conversely, the smaller the value of 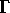 , the more slowly the
energy dissipates. Therefore, the correct answer is A.
, the more slowly the
energy dissipates. Therefore, the correct answer is A.
3. Two events occur 100 m apart with an intervening time interval
of 0.60 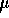 s. The speed of a reference frame in which they occur at the
same coordinate is:
s. The speed of a reference frame in which they occur at the
same coordinate is:
A) 0
B) 0.25c
C) 0.56c
D) 1.1c
E) 1.8c
Here we apply the Lorentz transformation for 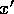 \
such that
\
such that

For 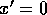 we have
we have 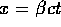 or
or 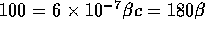 . Then it is easy to see that
. Then it is easy to see that 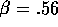 The correct answer is C.
The correct answer is C.
4. A wave traveling to the right on a stretched string is shown below. The direction of the instantaneous velocity of the point P on the string is:
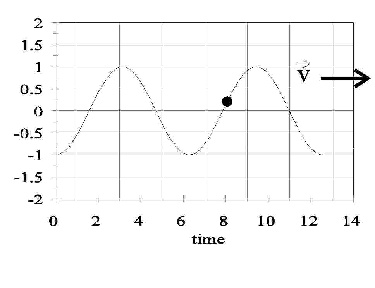
A) 
B) 
C) 
D) 
E) no direction since v = 0
This is quite hard. The wave moves to the right. The easiest thing to do is draw the wave at a later time, in which case we see that the point P has moved DOWN. Therefore, the point P is going to have a smaller value at later times than it has at the time shown. This means that the point P is moving DOWN. The correct answer is B.
5. A rocket ship of rest length 100 m is moving at speed 0.8c past a timing device which records the time interval between the passage of the front and back ends of the ship. This time interval is:
A) 0.20 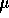 s
s
B) 0.25 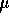 s
s
C) 0.33 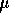 s
s
D) 0.52 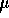 s
s
E) 0.69 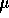 s
s
There are several ways to do this problem. The easiest, perhaps, is
to realize that, in our frame, the length of the rocket ship is 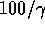 . So we have to find
. So we have to find 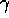 when
when 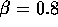 But this is not hard, and we get (plugging in the numbers) that
But this is not hard, and we get (plugging in the numbers) that 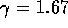 Thus the 100 meter rocket ship looks, to us, as
if it is L=60 meters long. But 60 meters at speed
Thus the 100 meter rocket ship looks, to us, as
if it is L=60 meters long. But 60 meters at speed 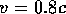 gives us a time of
gives us a time of 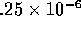 seconds.
The correct answer is B.
seconds.
The correct answer is B.
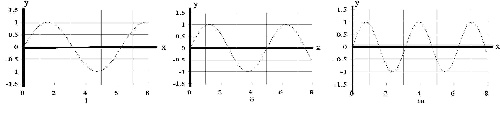
6. Three traveling sinusoidal waves are on identical strings, with
the same tension. The mathematical forms of the waves are 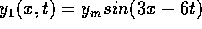 ,
, 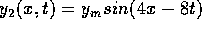 , and
, and 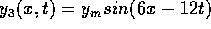 , where x is in meters and t is in seconds.
Match each mathematical form to the appropriate graph below.
, where x is in meters and t is in seconds.
Match each mathematical form to the appropriate graph below.
A)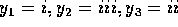
B) 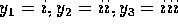
C) 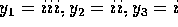
D) 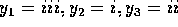
E) 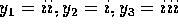
In these diagrams, for which you needed a magnifying glass to see
carefully, we are looking at a snapshot in time. Time is frozen so we are
looking at the wavelengths. We can see the wavelengths from the three
equations. In i, k=3 so 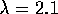 meters.
Similarly, for the next two diagrams,
meters.
Similarly, for the next two diagrams, 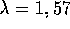 and
and 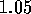 meters respectively. The shortest wavelength is
meters respectively. The shortest wavelength is 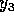 \
and the longest wavelength is
\
and the longest wavelength is 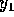 . This means
. This means 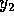 \
is in the middle. When we look at the diagrams, we see the longest
wavelength is i and the shortest is iii. So we identify
\
is in the middle. When we look at the diagrams, we see the longest
wavelength is i and the shortest is iii. So we identify 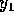 \
with i and
\
with i and 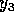 with iii. The correct answer is B.
with iii. The correct answer is B.
7. In the diagram below, the interval PQ represents:
A) wavelength/2
B) wavelength
C) 2 x amplitude
D) period/2
E) period
This is meant to be a simple problem in identification. The interval shown is the period, the distance between identical time points on the waveform. The correct answer is E.
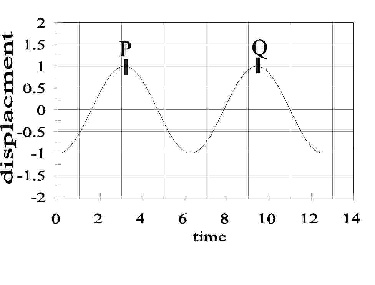
8. A sinusoidal wave is traveling toward the right as shown. Which letter correctly labels the wavelength of the wave?
A) A
B) B
C) C
D) D
E) E
Here we have a term identification problem again. The wavelength is A. so the correct answer here is A.
9. A particle is in simple harmonic motion along the x axis. The
amplitude of the motion is 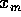 . When it is at
. When it is at 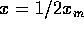 , its kinetic
energy is K = 5J and its potential energy (measured with U = 0 at x = 0) is
U = 3J. When it is at
, its kinetic
energy is K = 5J and its potential energy (measured with U = 0 at x = 0) is
U = 3J. When it is at 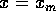 , the kinetic and potential energies are:
, the kinetic and potential energies are:
A) K = 5J and U = -3J
B) K = 0 and U = 8J
C) K = 8J and U = 0
D) K = 0 and U = -8J
E) K = 5J and U = 3J
The total energy of our oscillator is 8 Joules. It will
be a constant. Therefore, when 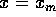 and the object is
instantaneously stopped, we have KE=0 and therefore PE=8
Joules. The correct answer is B.
and the object is
instantaneously stopped, we have KE=0 and therefore PE=8
Joules. The correct answer is B.
10. In a photoelectric effect experiment the stopping potential is:
A) the energy required to remove an electron from the sample
B) the kinetic energy of the most energetic electron ejected
C) the potential energy of the most energetic electron ejected
D) the photon energy
E) the electric potential that causes the electron current to vanish
This is a matter of definition. Stopping potential is just that, the potential at which the electron current STOPS. The correct answer is E.
11. A mass on a spring is subjected to a damping force that is proportional to its velocity and to an applied sinusoidal force. The energy dissipated by damping is supplied by:
A) friction
B) the kinetic of the mass
C) the applied force
D) gravity
E) the potential energy of the spring
Energy can only come from an external source. The key words are ``supplied by". The only external source is the applied force. The correct answer is C.
12. A sinusoidal force with a given amplitude is applied to an oscillator. At resonance the amplitude of the oscillation is limited by:
A) the damping force
B) the initial velocity
C) the force of gravity
D) the initial amplitude
E) none of the above
We have seen that the amplitude at resonance without damping is infinite. Therefore, it is damping (always present in reality) that prevents the amplitude from being infinite. The correct answer is A.
13. A 0.25-kg block oscillates on the end of the spring with a spring constant of 200 N/m. If the system has an energy of 6.0 J, then the amplitude of the oscillation is:
A) 0.06 m
B) 0.17 m
C) 0.24 m
D) 4.9 m
E) 6.9 m
At the end of its motion, when x=A all of the energy is potential. Then

Therefore we can solve and get 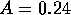 (we must not
forget that the arithmetic involves taking a square root of
(we must not
forget that the arithmetic involves taking a square root of 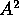 ). The correct answer is C.
). The correct answer is C.
14. A meson when at rest decays 2 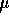 s after it is created. If
moving in the laboratory at 0.99c, its lifetime according to laboratory
clocks would be:
s after it is created. If
moving in the laboratory at 0.99c, its lifetime according to laboratory
clocks would be:
A) 4.6 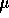 s
s
B) 14 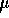 s
s
C) the same
D) 0.28 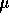 s
s
E) none of these
We always need to get 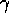 from
from 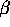 .
This is not hard and the arithmetic leads us to
.
This is not hard and the arithmetic leads us to 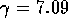 . But
this is the factor by which the lifetime is dilated so that, for us,
. But
this is the factor by which the lifetime is dilated so that, for us, 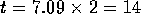
 s. The correct answer is
B.
s. The correct answer is
B.
15. A photon in light beam A has twice the energy of one in light beam B. The ratio A/B of the wavelengths is:
A) 1/2
B) 1/4
C) 1
D) 2
E) 4
We know that

Therefore, the ratio of wavelengths will be inverse to the ratio of
energies. Since the ratio of energies is TWO, the ratio of wavelengths is
ONE HALF The correct answer is A.
The correct answer is A.
16. An observer notices that a moving clock runs slow by a factor of exactly 10. The speed of the clock is:
A) 0.100c
B) 0.0100c
C) 0.990c
D) 0.900c
E) 0.995 c
This is easy. The dilation factor here is 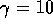 . We
can solve for
. We
can solve for 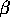 easily from this (careful with the
arithmetic though) and get
easily from this (careful with the
arithmetic though) and get 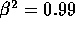 and
and 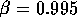 The correct answer is E.
The correct answer is E.
17. A measurement of the length of an object that is moving relative to the laboratory consists of noting the coordinates of the front and back:
A) at the same time according to clocks at rest in the laboratory
B) at the same time according to clocks that move with the object
C) at different times according to clocks at rest in the laboratory
D) at the same time according to clocks at rest with respect to the fixed stars
E) none of the above
We must measure the front and back of the stick at the same moment, the same instant of time, in our reference frame - i.e. the laboratory. Therefore, the correct answer is A.
18. In the accompanying figure all strings are the same except for
string D which has a greater linear density. Which of the answers below is
true? (The tensions are 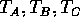 and
and 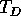 )
)
A) 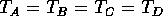
B) 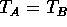 and
and 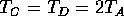
C) 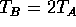 and
and 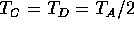
D) 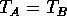 and
and 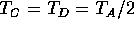
E) None of the above is true.
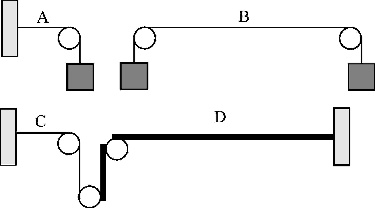
This is a basic mechanics problem. The tensions in A and B are the same because the wall supplies the same force as the left-hand weight in B. The tensions in C and D are also the same but they are 1/2 of the values in A\ and B. This is due to the fact that the same weight is supported by TWO strings and not by one string. Therefore, the correct answer is D.
19. Consider two strings, A and B with exactly the same linear
densities. String A has twice the tension of string B. The ratio of the
velocities of a wave propagated on string 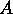 to that of string B (i.e.
to that of string B (i.e. 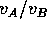 ) is
) is
A) 2
B) 1/2
C) 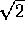
D) 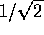
E) 4
This problem is related to the problem with weights and string densities above. If the densities are the same and we know that the velocity is given by

Therefore, the ratio of velocities is the SQUARE ROOT of the ratio
of the tensions. Since 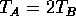 we have the ratio of the
velocities is
we have the ratio of the
velocities is 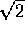 . The correct answer is C.
. The correct answer is C.
20. Consider two strings, A and B with exactly the same
tensions The linear density of string A is twice that for string 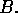 The
ratio of the velocities of a wave propagated on string
The
ratio of the velocities of a wave propagated on string 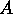 to that of
string B (i.e.
to that of
string B (i.e. 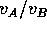 ) is
) is
A) 2
B) 1/2
C) 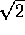
D) 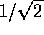
E) 4
Here we have the linear densities that are different. But, for
velocity, linear density occurs in the denominator. Therefore the higher the
linear density, the LOWER the velocity. The ratio of linear densities is TWO
so the ratio of velocities is 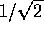 . The correct answer is
D.
. The correct answer is
D.